Improving Compressive Imaging Recovery via Measurement Augmentation
Improving Compressive Imaging Recovery via Measurement Augmentation
Jan 27, 2025·




Romario Gualdrón-Hurtado
Roman Jacome
Leon Suarez
Emmanuel Martinez
Henry Arguello

Abstract
In compressive imaging systems, the scene is acquired via linear coded noisy projections, known as measurements, requiring a recovery process to estimate the underlying signal. This recovery is inherently ill-posed, posing a challenge for accurate signal recovery. Existing methods that employ prior information about the signal often fail in practical scenarios. In this work, instead of developing a new prior over the signal, we exploit the structure of the low-dimensional measurements to synthesize an augmented measurement set that can be used in various recovery methods to improve its performance. We used a deep neural network to generate the synthetic measurements from the acquired data. We show the benefits of this approach in two schemes, deep learning-based recovery and the plug-and-play (PnP) algorithm. Particularly, our method is interpreted as a non-linear preconditioning technique for the PnP algorithm. We show improved performance for different sensing matrices.
Type
Publication
International Conference on Acoustics, Speech, and Signal Processing
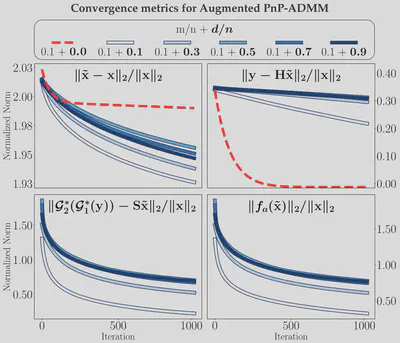
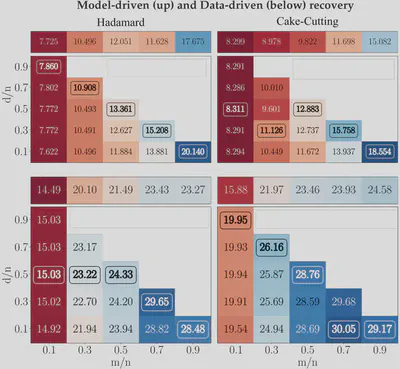
Simulation results